The view index nV is the first argument to srend_render() and all Srend calls, a number in 1:SREND_MAX_V. (SREND_MAX_V is set in the Srend.F90 definitions.) This is an index to data structures used by Srend internals which cache state and hold rendered data during processing. For a particular view, all other parameters except for the data, data dimensions, and data offsets will be identical.
The nV_out parameter is the view index for Compositing/Disk IO Image Finishing in case it is called by a process where rendering took place. If compose/finish is called on a process which does not render, nV_out can be the same as nV.
Note that right-handed xyz coordinates are used. It is up to the user to choose the up $\vec{U}$ vector. Below are the two common choices.
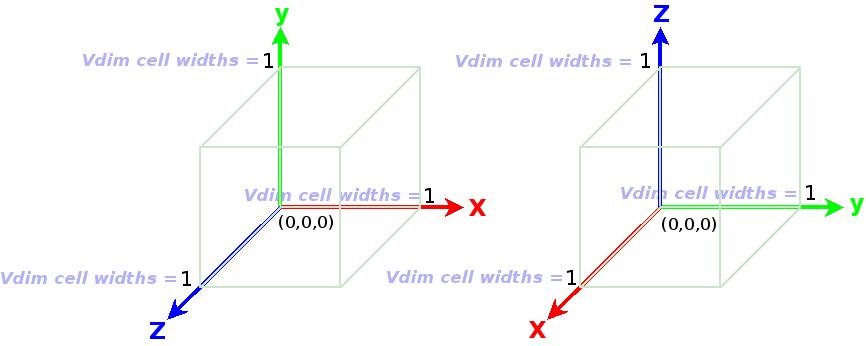
The data is always a 3D array in Cartesian 3D space, a box (right rectangular prism.). The data dimensions and offsets will always be integers, and the data is assumed to be cell-centered. There must always be a boundary of at least 1 surrounding data. For example, a 2x3x4 data array with a boundary of 1 (Bd=1) will have dimensions (0:3,0:4,0:5) or (1-Bd:2+Bd,1-Bd:3+Bd,1-Bd,4+Bd). The actual indices of the data will not matter so long as the shape is correct; (0:3,0:4,0:5) has the same shape as (1:4,1:5,1:6). The units for offsets in x,y, and z directions are cell widths. The cell (1,2,3) has one corner at (0,1,2) and another at (1,2,3). The data within cell (1,2,3) is centered at (0.5, 1.5, 2.5).
The entire volume box being rendered has one corner at (0,0,0) and the other at (xn,yn,zn) where xn,yn, and zn are the dimensions of the box and the number of cell widths spanning the volume box in each dimension. For purposes...
The parameter Vdim is the volume box dimension in cell widths used for purposes of the parameters which have object space dimensions. The Eye, eyeRight, xyz-clipping planes, and near & far clipping radii are in units of Volume box widths. For example, a $64^3$ volume box will use Vdim=64, then Eye = (/0.5, 0.5, 0.5/) is at the center (32,32,32) in cell width coordinates. If the volume box is not cubical, say 128x128x32, then Vdim=128 would scale the box to 1 x 1 x 0.25 for in the object space. Vdim is also used to adjust alpha for compositing in AMR use where Vdim increases with refinement. Directions here assume it is usual to set Vdim equal to the largest dimension in cell widths, but the user could do otherwise.
The angles are always in degrees. These are converted to radians internally for computation, of course.
The sampling increment dt is is units of cell widths where there are Vdim cells spanning the volume box. Thus, rendering uses the data resolution available. Past practice demonstrated by Woodward and Porter (U Minnesota LCSE) is that dt should be a fraction of cell width, say .5 to .25 with finer results available with .25 .
The nR parameter is the number of variable data arrays to render, all of exactly the same shape. There are then 1:nR color table offsets passed and 1:nR filenames passed, which are the essential differences between how variables are handled. Each variable is rendered sequentially, and all other viewing parameters are exactly the same for each. There might appear to be efficiency obtained by rendering all variables together along each ray as this reduces computation, but this did not increase speed in testing. There are efficiencies gained by reducing the amout of data pulled in for calculation.
tiles_right and tiles_down are both equal to 1 except for the mpi_tile mode designed for AMR data. When tiles_right*tiles_down > 1, this triggers mpi_tile mode which will have every rank call render_load() for each block, followed by render_flush() and tile_finish() by every rank. The TARGid parameter is an array of dimension (1:tiles_right, 1:tiles_down) which defines the MPI ranks used for compositing and writing out images by tile, but this array is just a (1:1,1:1) array containing an integer target MPI rank if there is just one tile.
The angle parameters alpha and beta are the horizontal and vertical angle spans for the spherical coordinate rendering, and these are in degrees.
$$0.0 \lt \alpha \le 360.0$$ $$0.0 \lt \beta \le 90.0$$The width W and height H of the output image are integer values in pixels. Both W and H must be divisible by 4. If "full spherical optimization" is selected, then W and H must both be divisible by 8. There are no checks on this. This restriction on user input could be overcome automatically by increasing the pixel dimensions to suit Srend requirements, then resizing the resulting image. However, the natural size imagery for most computer displays is divisible by sizable powers of 2, so this is probably not a heavy restriction.
Srend will reproject a final image to perspective if the parameter perspective=1 and certain reasonable conditions are met. If multiple shells are used, there will be no conversion to perspective because this makes little sense. "Full spherical optimization" only makes sense as spherical. If images are tiled, then there can be no reprojection to perspective until the images are montaged, but this reprojection will be done if SREND_TILE_MONTAGE is enabled and srend_tile_montage.F90 compiled to "montage" in the working path for Srend to call. In all cases, perspective projection makes no sense unless alpha and beta are both less than 180 degrees; this is not checked.
The polar far clip "pclip1" only renders for rays less that pclip1 degrees from the view direction vector. The default of 180.0 degrees clips nothing. A pclip1 value of 45.0 degrees results in a circular disk rendered, and alpha and beta must both be at least 90.0 degrees for this full disk to possibly be aparent. This clipping is useful for polar (North and South) renderings which can be resampled to spherical tilings at high and low altitudes. This is used for "full spherical optimization" because, otherwise, data toward poles would be heavily sampled for very little imagery. Such heavy sampling over little data is no problem for the resulting imagery, but it could be a problem for MPI ranks with data toward the poles as the rendering load would be much greater than for data in equatorial regions.